【初心者向け】Excelですぐに試せる『統計学入門』 データ分析に必要な基礎知識

どうも、TJです！（自己紹介はこちら）

初心者向け統計学入門ということで、データ分析をする上で必須となる基礎知識に加え、「Excelで実際に使うにはどうしたらいいのか？」をセットでまとめた内容になっています。

どうしても知識を得るだけだと現場での応用まで繋げられないことが多いかと思いますが、ぜひExcelで試しながら「こういう感じでやるのね」という感覚をつかんでいただければと思います。

↑Amazonでチェックする

分布の偏りを数値で表す

分布の偏りは「歪度」で表すことができます。

歪度が負なら右側に山があり、正なら左側に山がある分布になります。

データの散らばり具合を知る

尖度

データの散らばり具合を知る方法はいくつかありますが、まずは「尖度」を紹介します。

尖度が負なら平坦な分布、正なら尖った分布になります。

分散・標準偏差

分散とは「（各データ – 平均値）の2乗をすべて足して、データの個数で割ったもの」で、分散の平方根を取ったものが標準偏差になります。

要するに、平均値を基準とした場合の散らばり具合を数値化したもので、値が大きいほど散らばり具合が大きいと言えます。

また、それぞれ「標本分散/不偏分散」「標本標準偏差/不偏標準偏差」と、「標本」と「不偏」の2つのパターンがあります。

サンプルデータが母集団の全データの場合は「標本」で、サンプルデータが母集団の一部のデータの場合は「不偏」を使います。

ちなみに「偏差値」というのは「平均値50,標準偏差10の正規分布」のことで、自分の偏差値を「（自分の得点 – 平均点）/ 標準偏差 * 10 + 50」と計算すれば、自分の点数だと上から何%なのかが大体分かるという代物です。

ある程度の幅を持たせて平均や分散を推定する

例えば、「95%の確率でこの区間に平均値が収まる」のように、ある程度の幅を持たせて母集団の平均や分散を推定することを「区間推定」と呼びます。

それに対して、1つの値を使って母集団の平均や分散を推定することを「点推定」と呼びます。

母集団の分散が分かっている場合とそうでない場合で使用する関数が異なります。

2変数の相関関係の強さを知る

相関係数

相関関係とは「一方の値が増えれば他方の値も増えるという関係」のことで、その強さを表すのが「相関係数」です。

相関係数は-1~1の範囲で表現され、1に近いほど正の相関（一方が増えれば他方も増える）を、-1に近いほど負の相関（一方が増えれば他方は減る）をもち、0に近いほど無相関（関係がない）であるという意味になります。

注意すべきこととして、「相関関係≠因果関係」「疑似相関」の2点を覚えておきましょう。

前者についてですが、相関関係があるからと言って必ずしも因果関係があるとは言えないので、「Aが増えるとBも増えることが分かったので、Aを増やす施策を打ちましょう」と安易に考えるのはやめましょう。

後者について、「AとBの間に相関があると思ったら、実際はAとC、BとCの間に相関関係があった」という感じで、真の相関関係が別にあるのに、表面的に相関関係が見えてしまうことを疑似相関と呼びます。

相関係数の値から尚早に判断せず、他に隠れた要因がないか考えるクセをつけましょう。

ちなみに相関係数を求めるための数式では「x,yそれぞれの平均値に対する差（残差）の積を平均し、標準偏差で割る」という処理をしています。

正の相関の場合、x,yの残差はいずれも正になるので相関係数も正の符号を取り、負の相関の場合は負の符号を取ります。

さらに標準偏差で割っているのは、値を標準化することで-1~1の範囲に値を収めるためです。

さらに余談ですが、相関係数を2乗したものを「決定係数（寄与率）」と呼び、回帰式の当てはまりの良さを表す指標として使います。

数値を予測する

例えば、「気温が30℃の時のアイスクリームの売上個数を予測する」のように、ある変数をもとに他方の変数の値を予測することを「回帰」と呼びます。

この場合、気温を説明変数x、売上個数を目的変数yと呼んだりします。

目的変数に対して説明変数が1つの場合を単回帰分析、複数ある場合を重回帰分析といいます。

単回帰分析

重回帰分析

重回帰分析を利用する場合は、「似たような説明変数を使ってはいけない」ということに注意が必要です。

これを多重共線性と呼びますが、説明変数間に強い相関関係があると適切な予測結果を得られませんので、覚えておきましょう。

時系列分析

回帰分析が説明変数から目的変数を予測するものだったのに対し、過去の値から未来の値を予測することを時系列分析と呼びます。（説明変数と目的変数は同じです）

数値の差に意味があるのかを見極める

ABテストの結果、平均値で比べると差はついたけど、「本当に差があると言えるのかな？」なんてことよくありますよね。所謂、「有意差」ってやつです。

統計学では、この問題を解決するために「検定」を行います。

検定の手順は以下の通りです。

何やら難しそうな言葉が色々出てきましたね。笑

その名の通り、帰無仮説とは「無かったことにしたい仮説」のことです。

要するに、本心では「平均値に差がある」と主張したい場合に、それに対する帰無仮説「平均値に差がない」を棄てることで、主張が真実だとするのが検定と呼ばれる方法です。

なので、上の場合で言うと「主張したい仮説が対立仮説」、「捨てるのが間違ってる確率がp値」ということになります。

t値とp値

p値は検定統計量（t値）と呼ばれる値と以下の関数を使って求めることができます。

t値をざっくり説明すると「平均値の差/標準偏差」のような値で、「平均値の差が散らばり具合に対してどのぐらいの割合か」という意味です。

以下の図で言うと、平均の差が小さければt値は中央付近の値になり、平均の差が大きければ端の方の値になります。（引用元はこちら）

この時、色付けした部分の面積がp値になるので、平均の差が大きい場合はt値が大きくなりp値は小さくなる、つまり「平均の差に有意な差がある」ということになります。

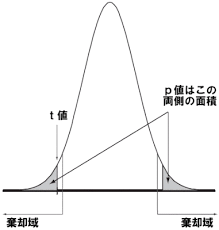
したがって、平均値の差が大きいように見えても、散らばり具合が大きいと差があるとは言いにくくなる、逆もまた然りということです。

t検定

上記で説明した内容と重複しますが、2グループ間の平均値に差があるかどうかを検定する場合にはt検定を用います。

前提として、母集団が正規分布に従っている場合に使うことができ、帰無仮説は「母集団の平均値は等しい」となります。

実は、上記の関数から得られた値がp値にあたります。この値が「p < 0.05」または「p < 0.01」となれば、対立仮説が採用されます。

また、関数の中にある「片側or両側」「検定の種類」に設定する数字は、対立仮説と母集団によって以下のように変わってきます。

ここで、「対応のあるデータ」とは「同じサンプルから得られた複数回の測定データ」のことを指します。

例えば、アンケート調査で同じ人がAとBの商品の点数を付けた場合、これは対応のあるデータです。

カイ二乗検定

「性別によって広告利用に差がある」など、2変数が独立であるかどうかを検定する場合によく用いられるのがカイ二乗検定です。

帰無仮説は「2変数は独立である」となります。

カイ二乗検定では、独立である場合の期待値と実測値の差がどのぐらいあるかによって検定を行います。

そのため、あらかじめクロス集計表を作成して期待値を求めておく必要があります。

相関関係の検定

2変数に相関関係があるかどうかを検定する方法もご紹介しておきます。

手順としては、「2変数に相関関係はない」という帰無仮説に対して、相関係数とデータ数からt値を求め、その値を以下の関数に入れてp値を求めます。

参考図書

↑Amazonでチェックする

さらに、統計学の歴史やその素晴らしさについて書かれた「統計学が最強の学問である」を要約したこちらの記事も併せてご覧ください。

【要約】5分で読める『統計学が最強の学問である』まとめ データ社会を生きぬくための武器と教養

どうも、TJです！（自己紹介はこちら）今回ご紹介するのは、「統計学が最強の学問である」です。発行部数50万部を超える大ベストセラーとなった本書から、「とりあえずこれ知ってたらドヤれまっせ」という内容に絞ってご紹介したいと思います。それではさ

tjblog.jp

2021.04.08